13. Meshing [Q&A Session]

Date/Time: 06 – 17 December 2021
All presentations are available in the virtual platform on-demand.

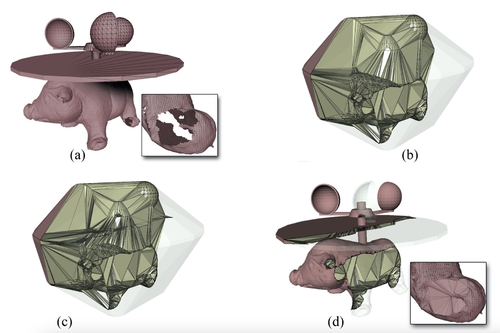
Convex polyhedral meshing for robust solid modeling

Abstract: We introduce a new technique to create a mesh of convex polyhedra representing the interior volume of a triangulated input surface. Our approach is particularly tolerant to defects in the input, which is allowed to self-intersect, to be non-manifold, disconnected, and to contain surface holes and gaps. We guarantee that the input surface is exactly represented as the union of polygonal facets of the output volume mesh. Thanks to our algorithm, traditionally difficult solid modeling operations such as mesh booleans and Minkowski sums become surprisingly robust and easy to implement, even if the input has defects. Our technique leverages on the recent concept of indirect geometric predicate to provide an unprecedented combination of guaranteed robustness and speed, thus enabling the practical implementation of robust though flexible solid modeling systems. We have extensively tested our method on all the 10000 models of the Thingi10k dataset, and concluded that no existing method provides comparable robustness, precision and performances.

Author(s)/Presenter(s):

---

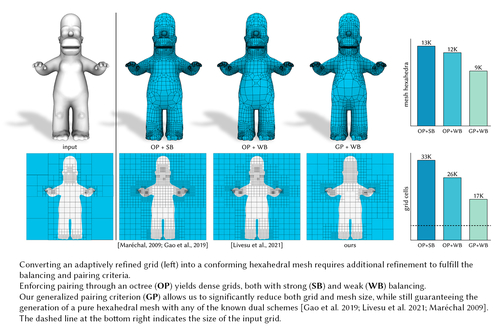
Generalized Adaptive Refinement for Grid-based Hexahedral Meshing

Abstract: Due to their nice numerical properties, conforming hexahedral meshes are considered a prominent computational domain for simulation tasks. However, the automatic decomposition of a general 3D volume into a small number of hexahedral elements is very challenging. Methods that create an adaptive Cartesian grid and convert it into a conforming mesh offer superior robustness and are the only ones concretely used in the industry. Topological schemes that permit this conversion can be applied only if precise compatibility conditions among grid elements are observed. Some of these conditions are local, hence easy to formulate; others are not and are much harder to satisfy. State-of-the-art approaches fulfill these conditions by prescribing additional refinement based on special building rules for octrees. These methods operate in a restricted space of solutions and are prone to severely over-refine the input grids, creating a bottleneck in the simulation pipeline. In this article, we introduce a novel approach to transform a general adaptive grid into a new grid meeting hexmeshing criteria, without resorting to tree rules. Our key insight is that we can formulate all compatibility conditions as linear constraints in an integer programming problem by choosing the proper set of unknowns. Since we operate in a broader solution space, we are able to meet topological hexmeshing criteria at a much coarser scale than methods using octrees, also supporting generalized grids of any shape or topology. We demonstrate the superiority of our approach for both traditional grid-based hexmeshing and adaptive polycube-based hexmeshing. In all our experiments, our method never prescribed more refinement than the prior art, and, in the average case, it introduced close to half the number of extra cells.

Author(s)/Presenter(s):

---

Interactive All-Hex Meshing via Cuboid Decomposition

Abstract: Standard PolyCube-based hexahedral (hex) meshing methods aim to deform the input domain into an axis-aligned PolyCube volume with integer corners; if this deformation is bijective, then applying the inverse map to the voxelized PolyCube yields a valid hex mesh. A key challenge in these methods is to maintain the bijectivity of the PolyCube deformation, thus reducing the robustness of these algorithms. In this work, we present an interactive pipeline for hex meshing that sidesteps this challenge by using a new representation of PolyCubes as unions of cuboids. We begin by deforming the input tetrahedral mesh into a near-PolyCube domain whose faces are close but not perfectly aligned to the major axis directions. We then build a PolyCube by optimizing the layout of a set of cuboids with user guidance to closely fit the deformed domain. Finally, we construct an inversion-free pullback map from the voxelized PolyCube to the input domain while optimizing for mesh quality metrics. We allow extensive user control over each stage, such as editing the voxelized PolyCube, positioning surface vertices, and exploring the trade-off among competing quality metrics, while also providing automatic alternatives. We validate our method on over one hundred shapes, including models that are challenging for past PolyCube-based and frame-field-based methods. Our pipeline reliably produces hex meshes with quality on par with or better than state-of-the-art. We additionally conduct a user study with 20 participants in which the majority prefer hex meshes they make using our tool to the ones from automatic state-of-the-art methods. This demonstrates the need for intuitive interactive hex meshing tools where the user can dictate the priorities of their mesh.

Author(s)/Presenter(s):

---

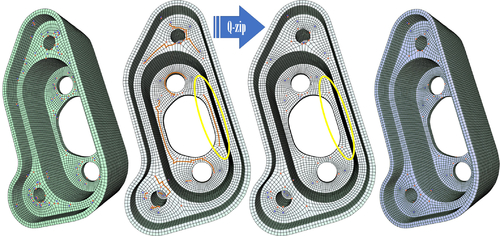
Q-zip: Singularity Editing Primitive for Quad Meshes

Abstract: Singularity editing of a quadrangle mesh consists in shifting singularities around for either improving the quality of the mesh elements or canceling extraneous singularities, so as to increase mesh regularity. However, the particular structure of a quad mesh renders the exploration of allowable connectivity changes non-local and hard to automate. In this paper, we introduce a simple, principled, and general quad-mesh editing primitive with which pairs of arbitrarily distant singularities can be efficiently displaced around a mesh through a deterministic and reversible chain of local topological operations with a minimal footprint. Dubbed Q-zip as it acts as a zipper opening up and collapsing down quad strips, our practical mesh operator for singularity editing can be easily implemented via parallel transport of a reference compass between any two irregular vertices. Batches of Q-zips performed in parallel can then be used for efficient singularity editing.

Author(s)/Presenter(s):

---

Back