17. Reconstruction [Q&A Session]

Date/Time: 06 – 17 December 2021
All presentations are available in the virtual platform on-demand.

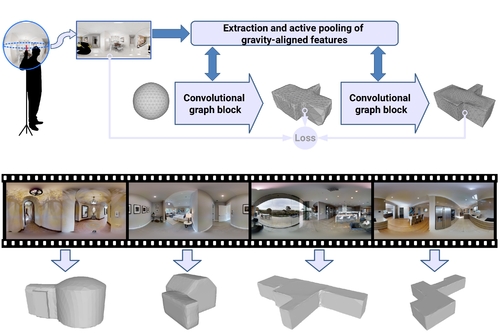
Deep3DLayout: 3D Reconstruction of an Indoor Layout from a Spherical Panoramic Image

Abstract: Recovering the 3D shape of the bounding permanent surfaces of a room from a single image is a key component of indoor reconstruction pipelines. In this article, we introduce a novel deep learning technique capable to produce, at interactive rates, a tessellated bounding 3D surface from a single $360^\circ$ image. Differently from prior solutions, we fully address the problem in 3D, significantly expanding the reconstruction space of prior solutions. A graph convolutional network directly infers the room structure as a 3D mesh by progressively deforming a graph-encoded tessellated sphere mapped to the spherical panorama, leveraging perceptual features extracted from the input image. Important 3D properties of indoor environments are exploited in our design. In particular, gravity-aligned features are actively incorporated in the graph in a projection layer that exploits the recent concept of multi head self-attention, and specialized losses guide towards plausible solutions even in presence of massive clutter and occlusions. Extensive experiments demonstrate that our approach outperforms current state of the art methods in terms of accuracy and capability to reconstruct more complex environments.

Author(s)/Presenter(s):

---

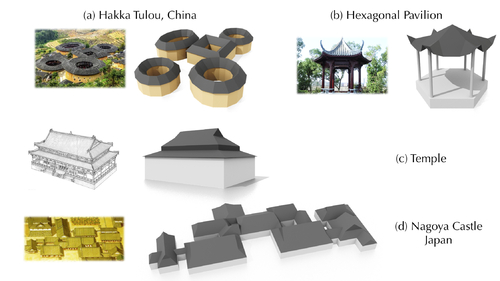
Intuitive and Efficient Roof Modeling for Reconstruction and Synthesis

Abstract: We propose a novel and flexible roof modeling approach that can be used for constructing planar 3D polygon roof meshes. Our method uses a graph structure to encode roof topology and enforces the roof validity by optimizing a simple but effective planarity metric we propose. This approach is significantly more efficient than using general purpose 3D modeling tools such as 3ds Max or SketchUp, and more powerful and expressive than specialized tools such as the straight skeleton. Our optimization-based formulation is also flexible and can accommodate different styles and user preferences for roof modeling. We showcase two applications. The first application is an interactive roof editing framework that can be used for roof design or roof reconstruction from aerial images. We highlight the efficiency and generality of our approach by constructing a mesh-image paired dataset consisting of 2539 roofs. Our second application is a generative model to synthesize new roof meshes from scratch. We propose to combine machine learning and our roof optimization techniques, by using transformers and graph convolutional networks to model roof topology, and our roof optimization methods to enforce the planarity constraint.

Author(s)/Presenter(s):

---

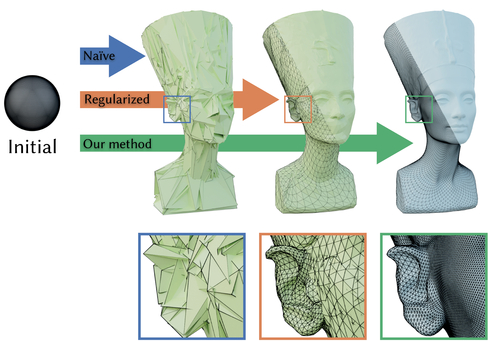
Large Steps in Inverse Rendering of Geometry

Abstract: Inverse reconstruction from images is a central problem in many scientific and engineering disciplines. Recent progress on differentiable rendering has led to methods that can efficiently differentiate the full process of image formation with respect to millions of parameters to solve such problems via gradient-based optimization. At the same time, the availability of cheap derivatives does not necessarily make an inverse problem easy to solve. Mesh-based representations remain a particular source of irritation: an adverse gradient step involving vertex positions could turn parts of the mesh inside-out, introduce numerous local self-intersections, or lead to inadequate usage of the vertex budget due to distortion. These types of issues are often irrecoverable in the sense that subsequent optimization steps will further exacerbate them. In other words, the optimization lacks robustness due to an objective function with substantial non-convexity. Such robustness issues are commonly mitigated by imposing additional regularization, typically in the form of Laplacian energies that quantify and improve the smoothness of the current iterate. However, regularization introduces its own set of problems: solutions must now compromise between solving the problem and being smooth. Furthermore, gradient steps involving a Laplacian energy resemble Jacobi's iterative method for solving linear equations that is known for its exceptionally slow convergence. We propose a simple and practical alternative that casts differentiable rendering into the framework of preconditioned gradient descent. Our preconditioner biases gradient steps towards smooth solutions without requiring the final solution to be smooth. In contrast to Jacobi-style iteration, each gradient step propagates information among all variables, enabling convergence using fewer and larger steps. Our method is not restricted to meshes and can also accelerate the reconstruction of other representations, where smooth solutions are generally expected. We demonstrate its superior performance in the context of geometric optimization and texture reconstruction.

Author(s)/Presenter(s):

---

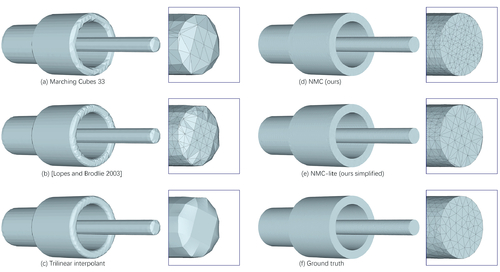
Neural Marching Cubes

Abstract: We introduce Neural Marching Cubes (NMC), a data-driven approach for extracting a triangle mesh from a discretized implicit field. Classical MC is defined by coarse tessellation templates isolated to individual cubes. While more refined tessellations have been proposed, they all make heuristic assumptions, such as trilinearity, when determining the vertex positions and local mesh topologies in each cube. In principle, none of these approaches can reconstruct geometric features that reveal coherence or dependencies between nearby cubes (e.g., a sharp edge), as such information is unaccounted for, resulting in poor estimates of the true underlying implicit field. To tackle these challenges, we re-cast MC from a deep learning perspective, by designing tessellation templates more apt at preserving geometric features, and learning the vertex positions and mesh topologies from training meshes, to account for contextual information from nearby cubes. We develop a compact per-cube parameterization to represent the output triangle mesh, while being compatible with neural processing, so that a simple 3D convolutional network can be employed for the training. We show that all topological cases in each cube that are applicable to our design can be easily derived using our representation, and the resulting tessellations can also be obtained naturally and efficiently by following a few design guidelines. In addition, our network learns local features with limited receptive fields, hence it generalizes well to new shapes and new datasets. We evaluate our neural MC approach by quantitative and qualitative comparisons to all well-known MC variants. In particular, we demonstrate the ability of our network to recover sharp features such as edges and corners, a long-standing issue of MC and its variants. Our network also reconstructs local mesh topologies more accurately than previous approaches.

Author(s)/Presenter(s):

---

Supervoxel Convolution for Online 3D Semantic Segmentation

Abstract: In this paper, we contribute a novel convolution operation directly on supervoxels, and achieve a new state-of-the-art online 3D semantic segmentation approach.

Author(s)/Presenter(s):

---

Back