14. Surface Parameterization and Texturing [Q&A Session]

Date/Time: 06 – 17 December 2021
All presentations are available in the virtual platform on-demand.

Computing Sparse Cones with Bounded Distortion for Conformal Parameterizations

Abstract: We propose a novel method to generate sparse cone singularities with bounded distortion constraints for conformal parameterizations. It is formulated as minimizing the ℓ0-norm of Gaussian curvature of vertices with hard constraints of bounding the distortion that is measured by the ℓ2-norm of the log conformal factor. We use the reweighted ℓ1-norm to approximate the ℓ0-norm and solve each convex weighted ℓ1 minimization subproblem by the Douglas-Rachford (DR) splitting scheme. To quickly generate sparse cones, we modify DR splitting by weighting the ℓ2-norm of the proximal mapping to force the small Gaussian curvature to quickly approach zero. Accordingly, compared with the conventional DR splitting, the modified method performs one to two orders of magnitude faster. Besides, we perform variable substitution of log conformal factors to simplify the computation process for acceleration. Our algorithm is able to bound distortion to compute sparse cone singularities, so that the resulting conformal parameterizations achieve a favorable tradeoff between the area distortion and the cone number. We demonstrate its effectiveness and feasibility on a large number of models.

Author(s)/Presenter(s):

---

Efficient and Robust Discrete Conformal Equivalence with Boundary

Abstract: We describe an efficient algorithm to compute a discrete metric with prescribed Gaussian curvature at all interior vertices and prescribed geodesic curvature along the boundary of a mesh. The metric is (discretely) conformally equivalent to the input metric. Its construction is based on theory developed in [Gu et al. 2018] and [Springborn 2020], relying on results on hyperbolic ideal Delaunay triangulations. Generality is achieved by considering the surface’s intrinsic triangulation as a degree of freedom, and particular attention is paid to the proper treatment of surface boundaries. While via a double cover approach the case with boundary can be reduced to the case without boundary quite naturally, the implied symmetry of the setting causes additional challenges related to stable Delaunay-critical configurations that we address explicitly. We furthermore explore the numerical limits of the approach and derive continuous maps from the discrete metrics.

Author(s)/Presenter(s):

---

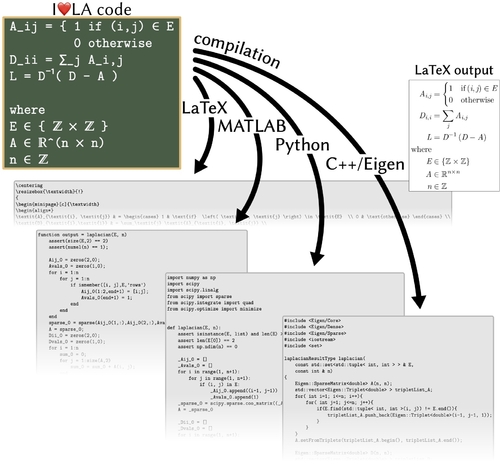
I❤️LA: Compilable Markdown for Linear Algebra

Abstract: Communicating linear algebra in written form is challenging: mathematicians must choose between writing in languages that produce well-formatted but semantically-underdefined representations such as LaTeX; or languages with well-defined semantics but notation unlike conventional math, such as C++/Eigen. In both cases, the underlying linear algebra is obfuscated by the requirements of esoteric language syntax (as in LaTeX) or awkward APIs due to language semantics (as in C++). The gap between representations results in communication challenges, including underspecified and irreproducible research results, difficulty teaching math concepts underlying complex numerical code, as well as repeated, redundant, and error-prone translations from communicated linear algebra to executable code. We introduce I❤️LA, a language with syntax designed to closely mimic conventionally-written linear algebra, while still ensuring an unambiguous, compilable interpretation. Inspired by Markdown, a language for writing naturally-structured plain text files that translate into valid HTML, I❤️LA allows users to write linear algebra in text form and compile the same source into LaTeX, C++/Eigen, Python/NumPy/SciPy, and MATLAB, with easy extension to further math programming environments. We outline the principles of our language design and highlight design decisions that balance between readability and precise semantics, and demonstrate through case studies the ability for I❤️LA to bridge the semantic gap between conventionally-written linear algebra and unambiguous interpretation in math programming environments.

Author(s)/Presenter(s):

---

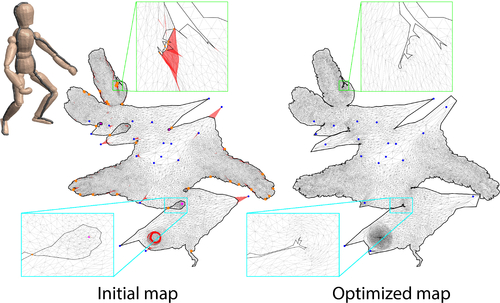
Optimizing Global Injectivity for Constrained Parameterization

Abstract: Injective parameterizations of triangulated meshes are critical across applications but remain challenging to compute. Existing algorithms to find injectivity either require initialization from an injective starting state, which is currently only possible without positional constraints, or else can only prevent triangle inversion, which is insufficient to ensure injectivity. Here we present, to our knowledge, the first algorithm for recovering a globally injective parameterization from an arbitrary non-injective initial mesh subject to stationary constraints. These initial meshes can be inverted, wound about interior vertices and/or overlapping. Our algorithm in turn enables globally injective mapping for meshes with arbitrary positional constraints. Our key contribution is a new energy, called smooth excess area (SEA), that measures non-injectivity in a map. This energy is well-defined across both injective and non-injective maps and is smooth almost everywhere, making it readily minimizable using standard gradient-based solvers starting from a non-injective initial state. Importantly, we show that maps minimizing SEA are guaranteed to be locally injective and almost globally injective, in the sense that the overlapping area can be made arbitrarily small. Analyzing SEA's behavior over a new benchmark set designed to test injective mapping, we find that optimizing SEA successfully recovers globally injective maps for 85% of the benchmark and obtains locally injective maps for 90%. In contrast, state-of-the-art methods for removing triangle inversion obtain locally injective maps for less than 6% of the benchmark, and achieve global injectivity (largely by chance as prior methods are not designed to recover it) on less than 4%.

Author(s)/Presenter(s):

---

TM-NET: Deep Generative Networks for Textured Meshes

Abstract: We introduce TM-NET, a novel deep generative model for synthesizing textured meshes in a part-aware manner. Once trained, the network can generate novel textured meshes from scratch or predict textures for a given 3D mesh, without image guidance. Plausible and diverse textures can be generated for the same mesh part, while texture compatibility between parts in the same shape is achieved via conditional generation. Specifically, our method produces texture maps for individual shape parts, each as a deformable box, leading to a natural UV map with minimal distortion. The network separately embeds part geometry (via a PartVAE) and part texture (via a TextureVAE) into their respective latent spaces, so as to facilitate learning texture probability distributions conditioned on geometry. We introduce a conditional autoregressive model for texture generation, which can be conditioned on both part geometry and textures already generated for other parts to achieve texture compatibility. To produce high-frequency texture details, our TextureVAE operates in a high-dimensional latent space via dictionary-based vector quantization. We also exploit transparencies in the texture as an effective means to model complex shape structures including topological details. Extensive experiments demonstrate the plausibility, quality, and diversity of the textures and geometries generated by our network, while avoiding inconsistency issues that are common to novel view synthesis methods.

Author(s)/Presenter(s):

---

Back