12: Geometry Processing and Simulation [Q&A Session]

Date/Time: 06 – 17 December 2021
All presentations are available in the virtual platform on-demand.

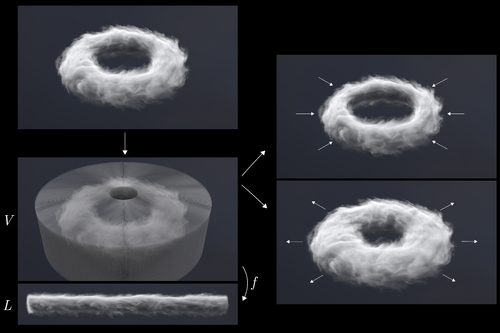
Generalized Fluid Carving With Fast Lattice-Guided Seam Computation

Abstract: In this paper, we introduce a novel method for intelligently resizing a wide range of volumetric data including fluids. Fluid carving, the technique we build upon, only supported particle-based liquid data, and because it was based on image-based techniques, it was constrained to rectangular boundaries. We address these limitations to allow a much more versatile method for volumetric post-processing. By enclosing a region of interest in our lattice structure, users can retarget regions of a volume with non-rectangular boundaries and non-axis-aligned motion. Our approach generalizes to images, videos, liquids, meshes, and even previously unexplored domains such as fire and smoke. We also present a seam computation method that is significantly faster than the previous approach while maintaining the same level of quality, thus making our method more viable for production settings where post-processing workflows are vital.

Author(s)/Presenter(s):

---

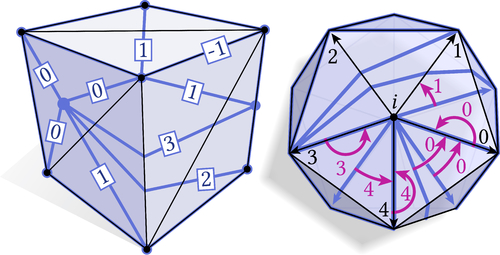
Integer Coordinates for Intrinsic Geometry Processing

Abstract: This paper describes a numerically robust data structure for encoding intrinsic triangulations of polyhedral surfaces. Many applications demand a correspondence between the intrinsic triangulation and the input surface, but existing data structures either rely on floating point values to encode correspondence, or do not support remeshing operations beyond basic edge flips. We instead provide an integer-based data structure that guarantees valid correspondence, even for meshes with near-degenerate elements. Our starting point is the framework of normal coordinates from geometric topology, which we extend to the broader set of operations needed for mesh processing (vertex insertion, edge splits, etc.). The resulting data structure can be used as a drop-in replacement for earlier schemes, automatically improving reliability across a wide variety of applications. As a stress test, we successfully compute an intrinsic Delaunay refinement and associated subdivision for all manifold meshes in the Thingi10k dataset. In turn, we can compute reliable and highly accurate solutions to partial differential equations even on extremely low-quality meshes.

Author(s)/Presenter(s):

---

Interactive Cutting and Tearing in Projective Dynamics with Progressive Cholesky Updates

Abstract: We propose a new algorithm for updating a Cholesky factorization which speeds up Projective Dynamics simulations with topological changes. Our approach addresses an important limitation of the original Projective Dynamics, i.e., that topological changes such as cutting, fracturing, or tearing require full refactorization which compromises computation speed, especially in real-time applications. Our method progressively modifies the Cholesky factor of the system matrix in the global step instead of computing it from scratch. Only a small amount of overhead is added since most of the topological changes in typical simulations are continuous and gradual. Our method is based on the update and downdate routine in CHOLMOD but, unlike recent related work, supports dynamic sizes of the system matrix and the addition of new vertices. Our approach allows us to introduce clean cuts and perform interactive remeshing. Our experiments show that our method works particularly well in simulation scenarios involving cutting, tearing, and local remeshing operations.

Author(s)/Presenter(s):

---

Locking-Proof Tetrahedra

Abstract: We propose a novel mixed FEM approach to simulating incompressible solids that alleviates the locking problem for tetrahedra by using linear shape functions for both displacements and pressure.

Author(s)/Presenter(s):

---

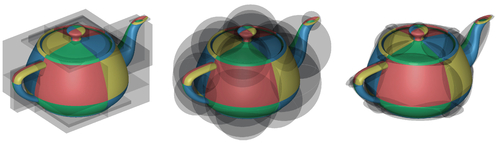
Sum-of-Squares Geometry Processing

Abstract: Geometry processing presents a variety of difficult numerical problems, each seeming to require its own tailored solution. This breadth is largely due to the expansive list of geometric primitives, e.g., splines, triangles, and hexahedra, joined with an ever-expanding variety of objectives one might want to achieve with them. With the recent increase in attention toward higher-order surfaces, we can expect a variety of challenges porting existing solutions that work on triangle meshes to work on these more complex geometry types. In this paper, we present a framework for solving many core geometry processing problems on higher-order surfaces. We achieve this goal through sum-of-squares optimization, which transforms nonlinear polynomial optimization problems into sequences of convex problems whose complexity is captured by a single degree parameter. This allows us to solve a suite of problems on higher-order surfaces, such as continuous collision detection and closest point queries on curved patches, with only minor changes between formulations and geometries.

Author(s)/Presenter(s):

---

Back