15. Curves and Surfaces [Q&A Session]

Date/Time: 06 – 17 December 2021
All presentations are available in the virtual platform on-demand.

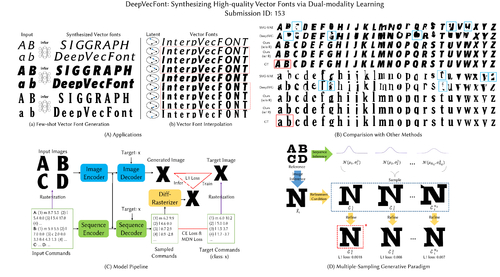
DeepVecFont: Synthesizing High-quality Vector Fonts via Dual-modality Learning

Abstract: Automatic font generation based on deep learning has aroused a lot of interest in the last decade. However, only a few recently-reported approaches are capable of directly generating vector glyphs and their results are still far from satisfactory. In this paper, we propose a novel method, DeepVecFont, to effectively resolve this problem. Using our method, for the first time, visually-pleasing vector glyphs whose quality and compactness are both comparable to human-designed ones can be automatically generated. The key idea of our DeepVecFont is to adopt the techniques of image synthesis, sequence modeling and differentiable rasterization to exhaustively exploit the dual-modality information (i.e., raster images and vector outlines) of vector fonts. The highlights of this paper are threefold. First, we design a dual-modality learning strategy which utilizes both image-aspect and sequence-aspect features of fonts to synthesize vector glyphs. Second, we provide a new generative paradigm to handle unstructured data (e.g., vector glyphs) by randomly sampling plausible synthesis results to get the optimal one which is further refined under the guidance of generated structured data (e.g., glyph images). Finally, qualitative and quantitative experiments conducted on a publicly-available dataset demonstrate that our method obtains high-quality synthesis results in the applications of vector font generation and interpolation, significantly outperforming the state of the art.

Author(s)/Presenter(s):
Yizhi Wang, Wangxuan Institute of Computer Technology, Peking University, China
Zhouhui Lian, Wangxuan Institute of Computer Technology, Peking University, China

---

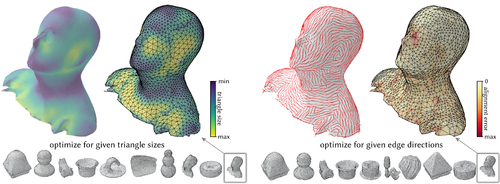
Differentiable Surface Triangulation

Abstract: Triangle meshes remain the most popular data representation for surface geometry. This ubiquitous representation is essentially a hybrid one that decouples continuous vertex locations from the discrete topological triangulation. Unfortunately, the combinatorial nature of the triangulation prevents taking derivatives over the space of possible meshings of any given surface. As a result, to date, mesh processing and optimization techniques have been unable to truly take advantage of modular gradient descent components of modern optimization frameworks. In this work, we present a differentiable surface triangulation that enables optimization for any per-vertex or per-face differentiable objective function over the space of underlying surface triangulations. Our method builds on the result that any 2D triangulation can be achieved by a suitably perturbed weighted Delaunay triangulation. We translate this result into a computational algorithm by proposing a soft relaxation of the classical weighted Delaunay triangulation and optimizing over vertex weights and vertex locations. We extend the algorithm to 3D by decomposing shapes into developable sets and differentiably meshing each set with suitable boundary constraints. We demonstrate the efficacy of our method on various planar and surface meshes on a range of difficult-to-optimize objective functions.

Author(s)/Presenter(s):
Marie-Julie Rakotosaona, LIX, École Polytechnique, France
Noam Aigerman, Adobe Research, United States of America
Niloy J. Mitra, Adobe Research, University College London (UCL), United Kingdom
Maks Ovsjanikov, LIX, École Polytechnique, France
Paul Guerrero, Adobe Research, United Kingdom

---

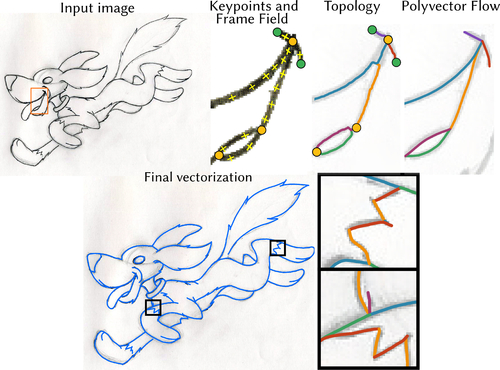
Keypoint-Driven Line Drawing Vectorization via PolyVector Flow

Abstract: Line drawing vectorization is a daily task in graphic design, computer animation, and engineering, necessary to convert raster images to a set of curves for editing and geometry processing. Despite recent progress in the area, automatic vectorization tools often produce spurious branches or incorrect connectivity around curve junctions; or smooth out sharp corners. These issues detract from the use of such vectorization tools, both from an aesthetic viewpoint and for feasibility of downstream applications (e.g., automatic coloring or inbetweening). We address these problems by introducing a novel line drawing vectorization algorithm that splits the task into three components: (1) finding keypoints, i.e., curve endpoints, junctions, and sharp corners; (2) extracting drawing topology, i.e., finding connections between keypoints; and (3) computing the geometry of those connections. We compute the optimal geometry of the connecting curves via a novel geometric flow --- PolyVector flow --- that aligns the curves to the drawing, disambiguating directions around Y-, X-, and T-junctions. We show that our system robustly infers both the geometry and topology of detailed complex drawings. We validate our system both quantitatively and qualitatively, demonstrating that our method visually outperforms previous work.

Author(s)/Presenter(s):
Ivan Puhachov, Université de Montréal, Canada
William Neveu, Université de Montréal, Canada
Edward Chien, Boston University, United States of America
Mikhail Bessmeltsev, Université de Montréal, Canada

---

Repulsive Curves

Abstract: We present efficient algorithms for self-repulsion of curves through minimization of the "tangent-point energy", providing a general-purpose tool for collision avoidance in shape optimization and design.

Author(s)/Presenter(s):
Christopher Yu, Carnegie Mellon University, United States of America
Henrik Schumacher, RWTH Aachen University, Germany
Keenan Crane, Carnegie Mellon University, United States of America

---

Repulsive Surfaces

Abstract: Geometric functionals that penalize bending or stretching of a surface play a key role in geometric modeling and digital geometry processing, but to date have ignored a very basic requirement: in many situations, surfaces must not pass through themselves. This paper develops a numerical framework for optimization of surface geometry while avoiding (self-)collision. The starting point is the tangent-point energy, which effectively pushes apart pairs of points that are close in space but distant along the surface. We develop a discretization of this energy for triangle meshes, and introduce a novel acceleration scheme based on a fractional Sobolev inner product. In contrast to similar schemes developed for curves, we avoid the complexity of building a multiresolution mesh hierarchy by decomposing our preconditioner into two ordinary Poisson equations, plus forward application of a fractional derivative. We further accelerate this scheme via hierarchical approximation, and describe how to incorporate a variety of constraints (area, volume, etc.). Finally, we explore how this machinery might be applied to applications in mathematical visualization and geometry processing.

Author(s)/Presenter(s):
Chris Yu, Carnegie Mellon University, United States of America
Caleb Brakensiek, Independent Researcher, United States of America
Henrik Schumacher, Aachen University, Germany
Keenan Crane, Carnegie Mellon University, United States of America

---

Back